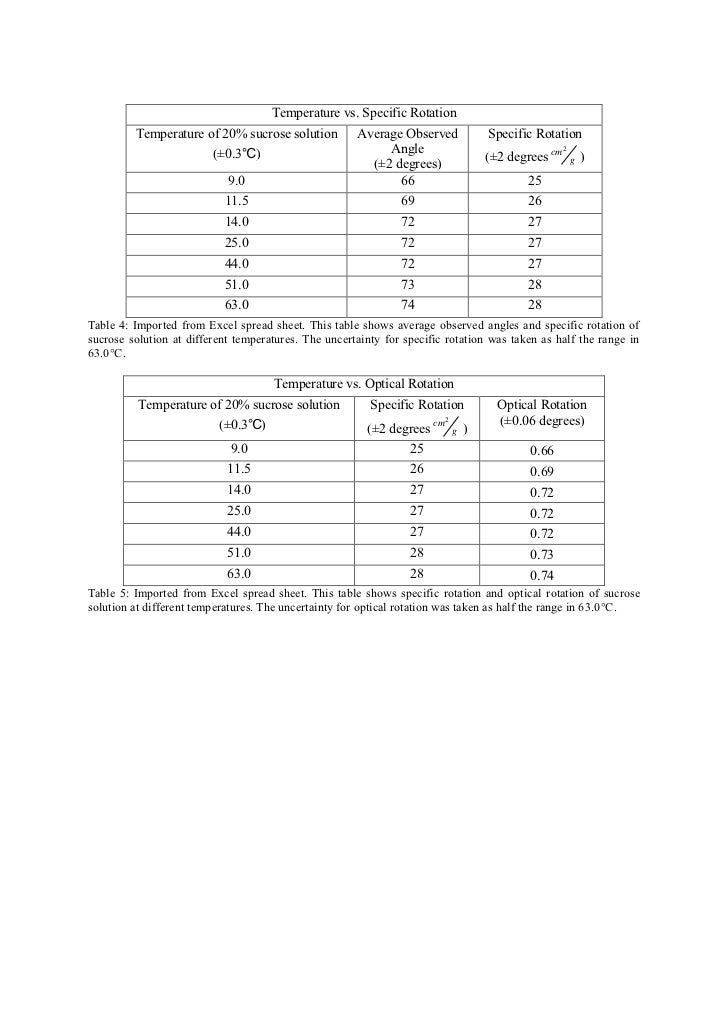
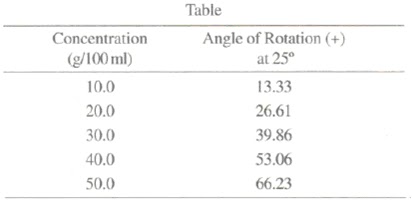
Specific Rotation Of Sucrose
Stereochemistry: Specific Rotation and Related Calculations. L = cell path length in decimeters. (1 decimeter = 1 dm = 10 cm. A standard polarimeter tube is 1.00 dm in length.) c = concentration in g ml -1 for a pure liquid compound (i.e., the liquid's density), or g 100 ml -1 for a solution. Armed with these facts. Sucrose is wiidespread in seeds, leaves, fruits, flowers and roots of plants, where it functions as an energy store for metabolism and as a carbon source for biosynthesis. The annual world production of sucrose is in excess of 90 million tons mainly from the juice of sugar cane (20%) and sugar beet (17%).
In chemistry, specific rotation ([α]) is a property of a chiralchemical compound.[1]:244 It is defined as the change in orientation of monochromaticplane-polarized light, per unit distance–concentration product, as the light passes through a sample of a compound in solution.[2]:2–65 Compounds which rotate the plane of polarization of a beam of plane polarized light clockwise are said to be dextrorotary, and correspond with positive specific rotation values, while compounds which rotate the plane of polarization of plane polarized light counterclockwise are said to be levorotary, and correspond with negative values.[1]:245 If a compound is able to rotate the plane of polarization of plane-polarized light, it is said to be “optically active”.
Specific rotation is an intensive property, distinguishing it from the more general phenomenon of optical rotation. As such, the observed rotation (α) of a sample of a compound can be used to quantify the enantiomeric excess of that compound, provided that the specific rotation ([α]) for the enantiopure compound is known. The variance of specific rotation with wavelength—a phenomenon known as optical rotatory dispersion—can be used to find the absolute configuration of a molecule.[3]:124 The concentration of bulk sugar solutions is sometimes determined by comparison of the observed optical rotation with the known specific rotation.
- 2Measurement
- 3Applications
Definition[edit]
The CRC Handbook of Chemistry and Physics defines specific rotation as:
For an optically active substance, defined by [α]θλ = α/γl, where α is the angle through which plane polarized light is rotated by a solution of mass concentration γ and path length l. Here θ is the Celsius temperature and λ the wavelength of the light at which the measurement is carried out.[2]
Values for specific rotation are reported in units of deg·mL·g−1·dm−1, which are typically shortened to just degrees, wherein the other components of the unit are tacitly assumed.[4] These values should always be accompanied by information about the temperature, solvent and wavelength of light used, as all of these variables can affect the specific rotation. As noted above, temperature and wavelength are frequently reported as a superscript and subscript, respectively, while the solvent is reported parenthetically, or omitted if it happens to be water.
2.5 ratio 1 gallon. 1 fluid ounce = 30 milliliters 8 ounces (1 cup) = 237 milliliters 16 ounces (1 pint) = 473 milliliters 32 ounces (1 quart) = 946 milliliters 64 ounces (½ gallon) = 1892 milliliters -or- 1.9 liters 128 ounces (1 gallon) = 3785 milliliters -or- 3.8 liters. Get the ratio. Example: 64:1 for 55 gallons, you would multiply the 2 ounces of chemical by 55 to get. 64=.195 or 19.5 cents per RTU gallon. 1:10 dilution selling at $7.30 per gallon- $7.30, 10=.73 or 73 cents per RTU. Gallon Helpful Tips. The smaller number in the ratio is the number of parts of concentrate, while the larger number is. The larger number represents the amount of gasoline, while the smaller is the amount of oil needed. If you are treating 1 gallon of clean unleaded gasoline, a 50:1 ration translates to 2.5 ounces of two-cycle oil, while preparing a 40:1 blend calls for 3 ounces of oil.
Measurement[edit]
| Compound name | [α]D20[deg dm−1 cm3 g−1] |
|---|---|
| (S)-2-Bromobutane | +23.1 |
| (R)-2-Bromobutane | −23.1 |
| D-Fructose | −92[5] |
| D-Glucose | +52.7[5] |
| D-Sucrose | +66.37[5] |
| D-Lactose | +52.3[5] |
| Camphor | +44.26[5] |
| Cholesterol | −31.5[5] |
| Taxol A | −49[6] |
| Penicillin V | +223[7] |
| Progesterone | +172[8] |
| Testosterone | +109[8] |
| (+)-Cavicularin | +168.2[9] |
| D-Hexol bromocamphorsulphonate | 2640[10][not in citation given] |
Optical rotation is measured with an instrument called a polarimeter. There is a linear relationship between the observed rotation and the concentration of optically active compound in the sample. There is a nonlinear relationship between the observed rotation and the wavelength of light used. Specific rotation is calculated using either of two equations, depending on whether the sample is a pure chemical to be tested or that chemical dissolved in solution.
For pure liquids[edit]
This equation is used:
In this equation, α (Greek letter 'alpha') is the measured rotation in degrees, l is the path length in decimeters, and ρ (Greek letter 'rho') is the density of the liquid in g/mL, for a sample at a temperature T (given in degrees Celsius) and wavelength λ (in nanometers). If the wavelength of the light used is 589 nanometers (the sodium D line), the symbol “D” is used. The sign of the rotation (+ or −) is always given.

- °
For solutions[edit]
For solutions, a slightly different equation is used:
In this equation, α (Greek letter 'alpha') is the measured rotation in degrees, l is the path length in decimeters, c is the concentration in g/mL, T is the temperature at which the measurement was taken (in degrees Celsius), and λ is the wavelength in nanometers.[11]
For practical and historical reasons, concentrations are often reported in units of g/100mL. In this case, a correction factor in the numerator is necessary:[1]:248[3]:123
When using this equation, the concentration and the solvent may be provided in parentheses after the rotation. The rotation is reported using degrees, and no units of concentration are given (it is assumed to be g/100mL). The sign of the rotation (+ or −) is always given. If the wavelength of the light used is 589 nanometer (the sodium D line), the symbol “D” is used. If the temperature is omitted, it is assumed to be at standard room temperature (20 °C).
For example, the specific rotation of a compound would be reported in the scientific literature as:[12]
- ° (c 1.00, EtOH)
Dealing with large and small rotations[edit]
If a compound has a very large specific rotation or a sample is very concentrated, the actual rotation of the sample may be larger than 180°, and so a single polarimeter measurement cannot detect when this has happened (for example, the values +270° and −90° are not distinguishable, nor are the values 361° and 1°). In these cases, measuring the rotation at several different concentrations allows one to determine the true value. Another method would be to use shorter path-lengths to perform the measurements.
In cases of very small or very large angles, one can also use the variation of specific rotation with wavelength to facilitate measurement. Switching wavelength is particularly useful when the angle is small. Many polarimeters are equipped with a mercury lamp (in addition to the sodium lamp) for this purpose.
Applications[edit]
Enantiomeric excess[edit]
If the specific rotation, of a pure chiral compound is known, it is possible to use the observed specific rotation, to determine the enantiomeric excess (ee), or 'optical purity', of a sample of the compound, by using the formula:[3]:124
For example, if a sample of bromobutane measured under standard conditions has an observed specific rotation of −9.2°, this indicates that the net effect is due to (9.2°/23.1°)(100%) = 40% of the R enantiomer. The remainder of the sample is a racemic mixture of the enantiomers (30% R and 30% S), which has no net contribution to the observed rotation. The enantiomeric excess is 40%; the total concentration of R is 70%.
However, in practice the utility of this method is limited, as the presence of small amounts of highly rotating impurities can greatly affect the rotation of a given sample. Moreover, the optical rotation of a compound may be non-linearly dependent on its enantiomeric excess because of aggregation in solution. For these reasons other methods of determining the enantiomeric ratio, such as gas chromatography or HPLC with a chiral column, are generally preferred.
Specific Rotation Of Sucrose Value
Hydrolysis Of Sucrose
Absolute configuration[edit]
The variation of specific rotation with wavelength is called optical rotatory dispersion (ORD). ORD can be used in conjunction with computational methods to determine the absolute configuration of certain compounds.[13]
References[edit]
- ^ abcVogel, Arthur I. (1996). Vogel's textbook of practical organic chemistry (5th ed.). Harlow: Longman. ISBN978-0582462366.
- ^ abHaynes, William M. (2014). CRC Handbook of Chemistry and Physics (95th ed.). CRC Press. ISBN9781482208672.
- ^ abcF. A. Carey; R. J. Sundberg (2007). Advanced Organic Chemistry, Part A: Structure and Mechanisms. Advanced Organic Chemistry (Fifth ed.). Springer. doi:10.1007/978-0-387-44899-2. ISBN978-0-387-44897-8.
- ^Mohrig, J. R.; Hammond, C. N.; Schatz, P. F. (2010). Techniques in Organic Chemistry (Third ed.). W. H. Freeman and Company. pp. 209–210.
- ^ abcdefR. C. Weast (1974). Handbook of Chemistry and Physics (55th ed.). CRC Press.
- ^'The Merck Index Online: Paclitaxel'. Royal Society of Chemistry. Retrieved 30 June 2014.
- ^'The Merck Index Online: Penicillin V'. Royal Society of Chemistry. Retrieved 30 June 2014.
- ^ abPaula Yurkanis Bruice (2012), Organic Chemistry, Pearson Education, Limited, p. 163, ISBN978-0-321-80322-1
- ^M. Toyota; et al. (1 July 1996). '(+)-Cavicularin: A novel optically active cyclic bibenzyl-dihydrophenanthrene derivative from the liverwort Cavicularia densa Steph'. Tetrahedron Letters. Elsevier. 37 (27): 4745–4748. doi:10.1016/0040-4039(96)00956-2. Retrieved 26 June 2014.
- ^A. Werner 'Über mehrkernige Metallammoniake' Chem. Ber. 1907, volume 40, pp. 2103–2125. doi:10.1002/cber.190704002126
- ^P. Y. Bruice (2011). Organic Chemistry (Sixth ed.). Prentice Hall. pp. 209–210.
- ^Coghill, Anne M.; Garson, Lorrin R. (2006). The ACS style guide (3rd ed.). Washington, D.C.: American Chemical Society. p. 274. doi:10.1021/bk-2006-STYG.ch013. ISBN978-0-8412-3999-9.
- ^Polavarapu, Prasad L. (2002). 'Optical rotation: Recent advances in determining the absolute configuration'. Chirality. 14 (10): 768–781. doi:10.1002/chir.10145. PMID12395394.
Articles
- Gta San Andreas Gratis Download
- Vijay Tv Shows Super Singer Junior 6 9/3/2019
- Dayz Single Player 2019
- Download Game Ultimate Ninja Storm
- Download Corel 2019 Torrent
- Dantdm Playing Minecraft Mods
- Paloma Mami Fingias Mp3
- Resident Evil 2 Remake Pc Download Completo
- Boot From Usb Acer
- Faster Ram On Digital Art Making
- Half Life 2 Gif
- D&d Homebrew Races
- Buod Ng Florante At Laura





